|
تنگ طه
وبلاگي شامل مطالب آموزشي دوره ابتدايي و مطالبي درباره روستاي تنگ طه
رابطه پيدا كردن مجموع جملات مجذور اعداد طبيعي به ترتيب از يك *************************************** رابطه پيدا كردن مساحت مثلث با كمك سه ضلع آن ***************************************
محاسبه تعداد مربعهاي موجود در يك شكل اگر شكل كلي ما مربع باشد براي محاسبه تعداد كل مربعهايي كه در شكل موجود مي باشد از اين روش استفاده مي نماييم . ابتدا تعداد مربعهاي طول مربع را مي شماريم و بعد آن را در خودش ضرب مي نماييم تا تعداد مربعهاي كوچك تك خانه اي پيدا شود . بعد يكي از اندازه طول كم مي نماييم و عدد را در خودش ضرب مي نماييم تا تعداد مربعهاي چهار خانه اي پيدا شود و اين كا را تا رسيدن به 1 ادامه مي دهيم و بعد همه جوابها را با هم جمع مي نماييم . مثلا مربعي كه هر ضلع آن از 7 مربع كوچك درست شده است ، كلا چند مربع دارد ؟ ابتدا از 7 شروع مي كنيم و آنرا در خودش ضرب مي نماييم مي شود 49 پس 49 تا مربع تك خانه اي داريم .بعد 6 را در 6 ضرب مي نماييم مي شود 36 كه تعداد مربعهاي 4 خانه اي مي باشد . ( البته مربع دو خانه و سه خانه نداريم .) بعد به همين ترتيب براي 5 و 4 و 3 و 2 و 1 هم عمل مي كنيم و جوابهاي 25 و 16 و 9 4 و 1 را به دست مي آوريم كه اگر همه را با هم جمع نماييم مي شود : 140 ***************************************
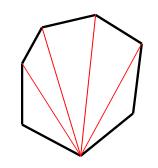
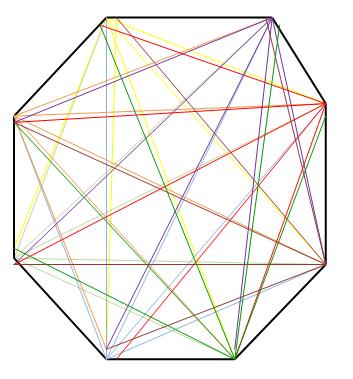
طريقه پيدا كردن مجموع زاويه هاي داخلي يك چند ضلعي 180 × ( 2- تعداد اضلاع ) اگر از يك رأس چند ضلعي به همه رأس هاي ديگر يك قطر رسم نماييم مشاهده مي كنيم كه تعدادي مثلث حاصل مي شود كه همه داراي فقط يك ضلع از چند ضلعي هستند به جز دو مثلث ابتدا و انتها كه هر كدام داراي دو ضلع چند ضلعي هستند . پس تعداد مثلثهاي ساخته شده برابر تعداد اضلاع چند ضلعي منهاي 2 مي باشد و چون مجموع زواياي مثلث برابر 180 درجه مي باشد بنابراين تعداد مثلثها را در 180 ضرب مي نماييم . *************************************** طريقه پيدا كردن تعداد قطرهاي يك چند ضلعي – 3 ) ÷ 2 تعداد ضلع (تعداد ضلع دليل آن : از هر رأس يك چند ضلعي مي توانيم يك پاره خط به همه رأس هاي ديگر رسم نماييم البته به دو رأس مجاور نمي شود رسم نمود و يكي هم كه خود رأس مي باشد كه به خودش نمي توان رسم نمود پس 3 تا از رأسها حذف شد پس تعداد اضلاع منهاي 3 و اين كار را براي همه اضلاع مي توانيم انجام دهيم پس آنرا در تعداد اضلاع ضرب مي نماييم . و چون همه قطرهايي كه به اين ترتيب رسم مي نماييم 2 بار تكرار مي شوند ( مثلا يكبار از رأس 1 به رأس 5 و يكبار از رأس 5 به رأس 1 رسم مي نماييم . ) آنرا بر 2 تقسيم مي نماييم .
*************************************** تعداد ارقام به كار رفته از 1 تا عدد معلوم تعداد ارقام = به تعداد ارقام عدد مورد نظر يك – تعداد ارقام عدد × ( 1 + عدد ) مثلا از 1 تا 2965 چند رقم به كار رفته است ؟ 10753 = 1111 – 4 × ( 1 + 2965 ) دليل آن : براي اعداد يك رقمي كه معلوم است هر كدام فقط يك رقم دارند و براي همه از 9 رقم استفاده مي شود براي اعداد 2 رقمي بايد از 10 تا 99 را حساب نماييم كه 90 عدد مي شود و بايد 90 را در 2 ضرب نماييم چون هر عدد دو رقم دارد و به همين ترتيب براي اعداد 3 رقمي كه از 100 تا 999 مي باشد و شامل 900 عدد مي باشد بايد 900 را در 3 ضرب نماييم و به همين ترتيب براي اعداد بالاتر . مثلا براي عدد چهار رقمي اگر عدد را در 4 ضرب نماييم تعداد ارقام پيدا مي شود اما كمي اضافه دارد كه اضافه آن براي اعداد 3 رقمي 900 تا مي شود چون خودشان 3 رقم دارند و ما 4 رقم حساب كرديم و براي اعداد 2 رقمي 180 = 90 × 2 تا اضافه داريم و براي اعداد 1 رقمي 27 = 9 × 3 كه اگر همه اضافه ها را با هم جمع نماييم 1107 مي شود و اگر براي بقيه اعداد هم همين كار را انجام دهيم متوجه مي شويم كه اگر عدد مورد نظر را 1 جمع نموده در تعداد رقمها ضرب نماييم و از حاصل عددي كه به تعداد ارقام يك درست شده كم نماييم ، تعداد ارقام مورد نياز براي نوشتن اعداد به دست مي آيد . *************************************** محاسبه زاويه بين عقربه ساعت شمار و دقيقه شمار براي محاسبه زاويه بين عقربه ساعت شمار و دقيقه شمار چون صفحه ساعت 360 درجه بوده و به 12 قسمت تقسيم شده پس هر ساعت برابر 30 درجه مي باشد . و چون هر ساعت 60 دقيقه مي باشد هر يك دقيقه كه عقربه ساعت شمار جلو برود به اندازه نيم درجه حركت كرده و البته عقربه دقيقه شمار در هر دقيقه 6 درجه جلو مي رود چون در 60 دقيقه 360 درجه حركت مي كند . پس اختلاف ميزان حركت عقربه ها در يك دقيقه برابر 5/5 درجه مي باشد . پس نحوه محاسبه زاويه بين دو عقربه به اين ترتيب است كه تعداد دقيقه را در 5/5 ضرب كرده و تعداد ساعت را در 30 ضرب مي نماييم و اختلاف اين دو مي شود زاويه بين دو عقربه . البته گاهي اين زاويه ، زاويه وارونه را نشان مي دهد كه مي توان 360 را از آن كم نمود تا به اندازه زاويه مورد نظر رسيد . كه اين بيشتر براي ساعتهاي بالا مانند 11 و 12 مي باشد . مثال : فاصله زاويه دو عقربه در ساعت 2 و 45 دقيقه (45 × 5/5 ) – ( 2 × 30 ) = 186/5
نظرات شما عزیزان:
مطالب جالبی بودن .
آخرین مطالب آرشيو وبلاگ پيوندها تبادل لينك هوشمند نويسندگان
|
||||||||||||||||
|
|
||||||||||||||||
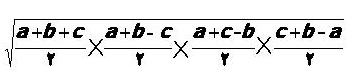


 آمار
وب سایت:
آمار
وب سایت: